浅谈,在理论上倍投是不是一定赚?
倍投只存在于理论中,只有在赌资、赌注、时间无限的情况下有意义,三个要素只要有一个不满足就是无意义的,显然,现实世界中这三个条件中任意一个都不能被满足。赌博是反直觉的,倍投也是反直觉的,倍投其实并不会让你赚更多,但是同样的,也不会让你亏更多。
概率很大,但是期望仍然是负的
单纯的概率是没有意义的,赌博是为了赢钱,必须加上收益期望才有意义。
拿抛硬币为例,胜率½,玩6轮,从1开始投注。学过小学数学的人会知道,连输6场的概率是1/64,也就是1.5625%。在倍投法中,只要赢一次就能获得收益,因此获得收益的概率为1-1/64,约为98.4375%。看上去是稳赚的,但是这没有意义,因为期望仍然是非正数。
在上面这个简单例子中,假如你赢了一次就跑,你有1/64的几率输掉63元,然后有63/64的几率赚1元。计算期望为1×63/64-63×1/64,结果为0元。
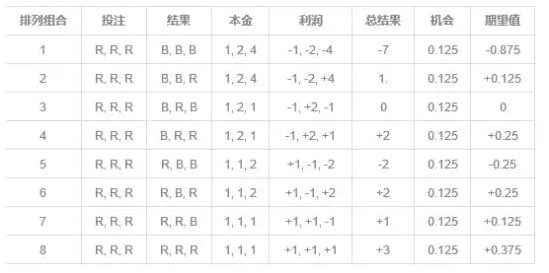
如果你赢了不停,继续下注1元,结果相同。这个也是反直觉的,并不会像赌客所想的那样赢更多,也不会像普通人那样见好不收会亏更多。公式证明有点麻烦,出于篇幅问题,借用一张图片,把规模缩小到3轮,这是轮盘赌红蓝球用倍投法的排列组合。把最右边的期望加起来,其实还是0。
*天鹅其实很常见
倍投基于一个假设,连输的概率很低,但是只要赢一次就能翻本。因此在交替输赢的局面下,倍投可以有较稳定的收益,直到遇到连输才会爆仓离场。但是连输的概率在多轮赌局后,就会非常大。这个很反直觉,但是确实是这样的。比如在上面的抛硬币赌局里,6场里连输6场概率是1.5625%,这个很容易计算出来。但是如果继续玩下去,玩10场、100场、200场呢?通过程序计算排列组合以及随机模拟,可以得出以下结果。代码在最后边。
为了让结果更有趣味性,我还加了记录模拟过程中出现过的最大连输数,这个最大连输次数主要和模拟次数有关。由于计算排列组合的时间复杂度是按指数增加的,超过20局以上就会耗时非常长,因此后续没有列出。
胜率为0.50,10000000次数模拟中,
每6次赌局中平均至少出现一次连输6次发生概率:1.56%,出现过的最多次连输:6次
胜率为0.5,通过排列组合,
每6次赌局中平均至少出现一次连输6次发生概率:1/64,1.56%
胜率为0.50,10000000次数模拟中,
每10次赌局中平均至少出现一次连输6次发生概率:4.68%,出现过的最多次连输:10次
胜率为0.5,通过排列组合,
每10次赌局中平均至少出现一次连输6次发生概率:48/1024,4.69%
胜率为0.50,10000000次数模拟中,
每50次赌局中平均至少出现一次连输6次发生概率:31.41%,出现过的最多次连输:28次
胜率为0.50,10000000次数模拟中,
每100次赌局中平均至少出现一次连输6次发生概率:54.47%,出现过的最多次连输:29次
胜率为0.50,10000000次数模拟中,
每200次赌局中平均至少出现一次连输6次发生概率:79.93%,出现过的最多次连输:31次
胜率为0.50,10000000次数模拟中,
每1000次赌局中平均至少出现一次连输6次发生概率:99.97%,出现过的最多次连输:32次
总结
赌博中使用倍投的期望只取决于赌局胜率,也就是说倍投并不能改变任何期望。
不过有些问题仍然萦绕不去。在较短期的赌局中,拥有较大的赌资和较小的赌注,确实可以使得胜率非常高,即使此时期望仍然为非正数。比如上面的例子,有98.4375%的几率赢1元,仅有1.5625%的几率输掉63元。总体胜率如此之高,这很让人迷惑,如何说服我不使用倍投?
在某种程度上,这确实呈现出一种悖论,其中期望为非正数是事实,而总体胜率却异常高。这种情况令人容易受到短期内高胜率的吸引。因此,很多网站提到的“在短期内,使用倍投法以小博大是有意义的”也有其合理之处。不过根据上面的计算我们知道,这个悖论不会持续太久,只要时间久一点,*天鹅就很容易遇见。